Making our first qubit

Computers encode information in units called ‘bits’. Bits have two possible states, 1 or 0. Physically, these correspond to the state of the computer’s electronics, like high or low voltage or current. Stringing bits together lets the computer represent systems with a greater number of states. For example, you can label four states with the bit strings ’00’, ‘01’, ‘10’, and ‘11’.

In most quantum computers, information is also represented in binary, and the two-state units of information are called ‘qubits’. We write qubit states in the Dirac notation as |0> and |1>. In an ion trap quantum computer, qubits are typically encoded in two of the ion’s atomic energy levels. The ion’s energy can be manipulated using electromagnetic fields, so we can perform computations on our qubit with RF signals.

Of course, none of this knowledge is of consequence if you don’t apply it to a system in the real world. But recently, our group has done just that: we have made our first qubit!

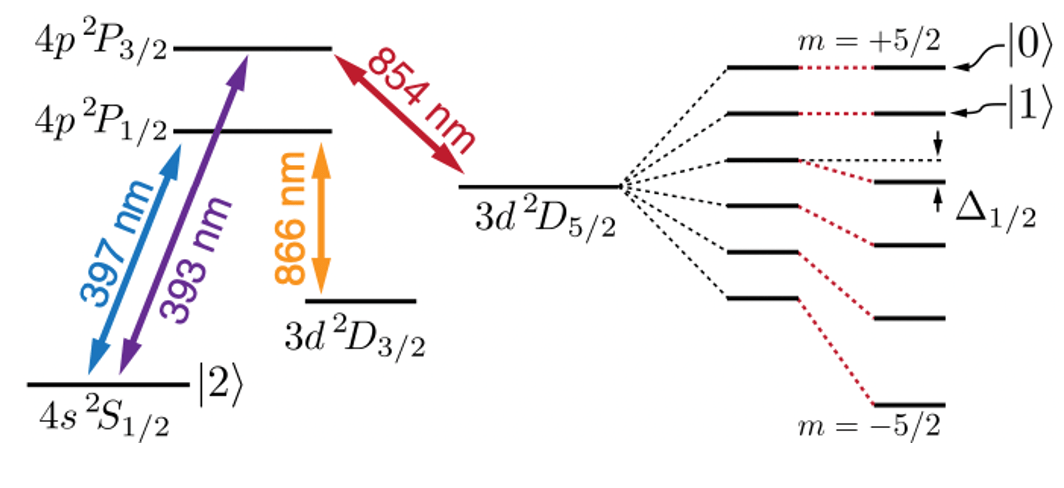
We chose to encode our qubit in two of the Zeeman sublevels of the metastable (1.17 s lifetime) D_5/2 manifold (a collection of states with a certain energy and orbital angular momentum) of a calcium-40 ion (⁴⁰Ca⁺); specifically, |0> corresponds to the m = +5/2 sublevel and |1> to the m = +3/2 sublevel. We are interested in this metastable qubit because we believe it affords several advantages over standard schemes which have at least one of the qubit states encoded in the ground S_1/2 manifold (see here and here for details). While such qubits have already been created and tested to some extent, the creation of our first qubit is an achievement for our lab (which only began trapping in October) and heralds our deeper investigation of the metastable qubit scheme.

To prepare our qubit, we began by applying a static magnetic field to the ion. This induces Zeeman shifts in the energy of the sublevels, which lifts the degeneracy of the states (i.e., creates a difference in energy between the sublevels). Then we used lasers to pump population out of the S_1/2 ground manifold and the D_3/2 manifold. When we chose the right laser polarizations and pumped long enough, we got ~99% of the population into the m = +5/2 sublevel of D_5/2.

Now we needed a way to control the qubit. Since all adjacent Zeeman sublevels have the same splitting, we have to lift the degeneracy of the transitions to ensure we only drive the qubit. We accomplished this by applying an 854 nm laser beam with a polarization that couples all sublevels besides the qubit states to the P manifolds. This creates a Stark shift in the energy of the affected states which is large enough to isolate them from the qubit. The action of the Stark shift on the sublevels is shown in the figure below.

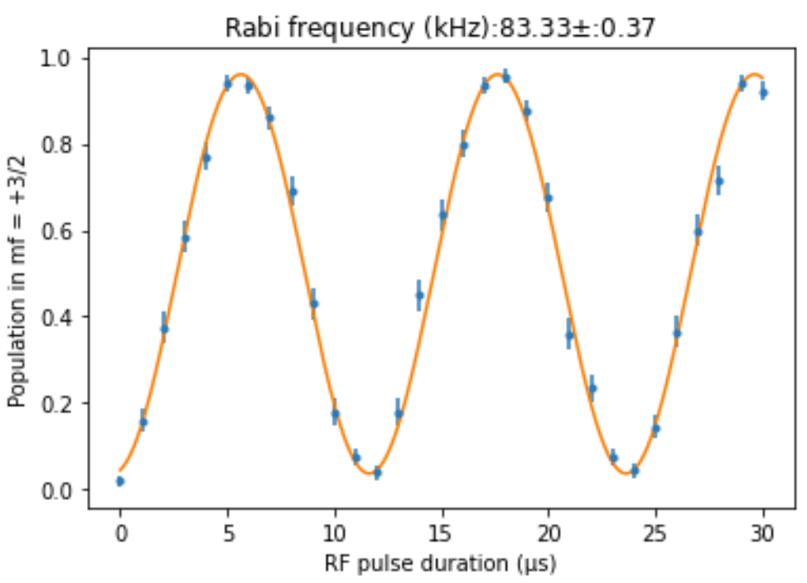
After all this preparation, our qubit was ready to go. We performed a quantum logic gate by applying an RF signal tuned to the qubit separation frequency. We used this to drive population oscillations (called ‘Rabi flops’) between our two qubit states and measured the population in one of the states as a function of the duration of the RF pulse. In this situation, we expect population to transfer sinusoidally between the two qubit states, i.e., the population in |0> will go as cos(Ωt) and the population in |1> will go as sin(Ωt), where ‘Ω’ is called the Rabi frequency. The process of measuring the qubit state is called ‘readout’, and we achieved it by hitting the ion with a specifically polarized laser beam to selectively pump population out of all Zeeman levels in D_5/2 except for m = +5/2. After this, we checked for fluorescence on the S_1/2 ↔ P_1/2 transition. The fraction of experiments in which we detected fluorescence told us how often the qubit was in the state |1> (m = +3/2).

In the plot below, you can see that we were able to achieve Rabi flopping at a rate (Rabi frequency) of 83.33 kHz. Our measurements and error bars are in blue and our fit to the data is in orange. On the timescale shown, we achieve clean sine-squared behavior. However, if we continued for a long time, we would observe the troughs of the curve asymptotically approaching 1, due to the finite lifetime of the D_5/2 manifold.